Ein abstrakter und zum Teil hilfreicher Einblick in mathematische Grundlagen.

Was folgt, ist eine Erklärung der Ideen und Methoden hinter der Analyse und Verwendung von Ellipsen. Lassen Sie sich von den Gleichungen nicht abschrecken, sie sind nur dazu da, um die Sprache für einige zu vereinfachen und von anderen ignoriert zu werden. Überspringen Sie einfach die Mathematik, falls sie Sie nicht anspricht, aber ehrlich gesagt wie könnte das sein?

Geometrisch gesehen ist eine Ellipse eine bestimmte Sorte Oval. Es kann als Verallgemeinerung des Kreises betrachtet werden, und als solcher gehört es zu den Kegelschnitten: Kreis, Ellipse, Parabel, Hyperbel.

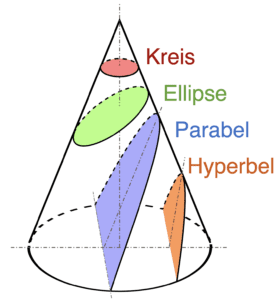Wie man in der Abbildung sehen kann, entsteht ein Kreis als Sonderfall genau dann, wenn eine Ebene einen Kegel senkrecht zu seiner Achse schneidet. Jede andere geschlossene Kurve, die sich aus dem Schnittpunkt einer Ebene mit einem Kegel ergibt, wird Ellipse genannt. Grob genommen könnte man sagen, dass Ellipsen Kreise mit zwei Zentren sind; genauer werden diese zwei Zentren Brennpunkte genannt.

Die formelle geometrische Definition ist folgende: Eine Ellipse ist der geometrische Ort aller Punkte der Ebene, für die die Summe der Abstände zu zwei gegebenen Punkten und gleich einer gegebene Konstante ist. Diese Konstante wird üblicherweise mit bezeichnet. Die Punkte und heissen Brennpunkte. In genauer mathematischer Sprache:

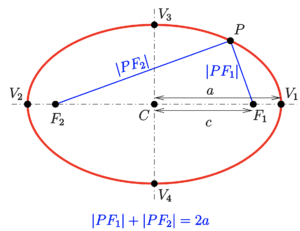Um darüber reden zu können, braucht man zusätzlich einige Definitionen:

• der Punkt in der Mitte von und heisst Mittelpunkt der Ellipse;
• die Gerade durch und heisst Hauptachse;
• und die dazu senkrechte Gerade durch heisst Nebenachse;
• den Abstand nennt man grosse Halbachse.

Im Bild (nicht markiert) wäre der Abstand zwischen und die kleine Halbachse. Führt man noch ein kartesisches Koordinatensystem in die Ebene ein, kann man der Ellipse auch eine analytischere Definition geben. Man nennt -Achse die “horizontale” Achse, und -Achse die “vertikale”. Sie treffen sich in – dem Koordinatenursprung. Jeder Punkt in der Ebene ist genau bestimmt durch seine Koordinaten . Zum Beispiel liegt der Punkt Einheiten nach rechts und Einheit nach oben, und der Punkt Einheiten nach links und Einheiten nach unten.

Jetzt kann man sagen, dass die Ellipse mit grosser Halbachse und kleiner Halbachse aus allen Punkten besteht, die die folgende Gleichung erfüllen:

Diese Gleichung kann durch einfache Anwendung des Satzes des Pythagoras und ein bisschen Gleichung-Jonglage erreicht werden. Viel Spass dabei!

Es ist hilfreich anzumerken, dass in dem häufigeren Fall, in dem die Ellipse eher zufällig in der Ebene liegt und nicht im Ursprung zentriert und “schön” orientiert ist, die Gleichung etwas komplizierter wird und etwa so aussieht: , wo beliebige Konstanten sind. Das ist in der Tat die allgemeine Gleichung für jeden Kegelschnitt in der Ebene.

Um sich an die Gleichung gewöhnen zu können, hilft es anzumerken, dass falls , für ein beliebiges , und man eine Ellipse in dem Koordinatenursprung betrachtet, sich die Gleichung vereinfacht in der eines Kreises mit Radius darstellen lässt:

Folgendes wird benötigt: Für beliebige fünf Punkte in der Ebene, von denen keine drei kollinear sind (auf einer Linie), gibt es einen einzigen Kegelschnitt, der sie alle berührt. Der Beweis dafür benötigt ein viel tieferes Verständnis für Mathematik und die Website eines Geigenbauers ist kein Ort dafür. Spannenderweise benutzt es eine Methode, die von dem schweizer Mathematiker Jakob Steiner entwickelt wurde. (Freund von Jacobus Stainer? Zufall?)

Zurück zur Realität.

Gesucht wurde die genaue Ellipse, die durch die folgenden fünf Punkte des C-Bügels eines Panormo-Models läuft:

• die zwei Punkte auf der horizontalen Linie, welche die obere Ecke schneidet (d. h. die obere Ecke selber und ein Punkt weiter innen);
• die zwei Punkte auf der horizontalen Linie, weche die untere Ecke schneidet (d.h. die untere Ecke selber und ein Punkt weiter innen);
• den Punkt der schmalste Stelle des C-Bügels.

Nachdem diese fünf Punkte in einem Koordinatensystem eingesetzt wurden, hat man ein Gleichungssystem aus Gleichungen der Form konstruiert. Die Lösung dieses Gleichungssystems erlaubt die Bestimmung der grossen und kleinen Halbachse. Somit kann die gesuchte Ellipse gezeichnet werden. Unten sieht man schöne Methoden, um das zu tun, um aber möglichst präzise zu sein, wurde diese Ellipse auch geplottet (mit Geogebra) und ausgeschnitten. Diese Schablone wurde schlussendlich für den Umriss des Basses benutzt. Obere und untere Flanke bestehen aus Kreissegmenten, alle anderen Kurven (Oberklotz, Ecken und C-Bügel) wurden mithilfe dieser Ellipse gezeichnet.

Jetzt einmal tief ein- und ausatmen…

Sobald die Ellipse definiert wurde, ist es wichtig zu beobachten, dass es sich nicht nur um eine reine theoretische Konstruktion handelt, sondern dass sie sehr häufig in der Natur zu finden ist. Auch wurde sie seit Jahrhunderten in der Architektur benutzt und seit Jahrtausenden ist sie bekannt und verstanden.

Das bekannteste Beispiel dafür ist unser Solarsystem. Jeder Planet folgt einer elliptischen Umlaufbahn um die Sonne herum, die auf einer der zwei Brennpunkte dieser Ellipse liegt.

Genauer gesagt folgen zwei Körper, die gravitativ gebunden sind, ähnlichen elliptischen Umlaufbahnen und ihr Baryzentrum liegt in einem Brennpunkt deren Ellipse.

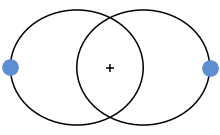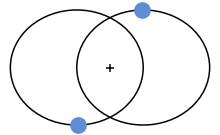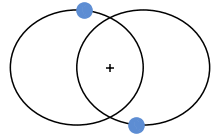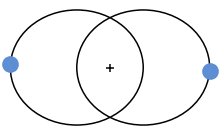Der Sonderfall unseres Sonnen-Erde-Systems ist durch die extreme Masse der Sonne bestimmt. Sie ist so viel massiver als die Erde, und so viel grösser, dass der Brennpunkt der elliptischen Bahn innerhalb der Sonne liegt. Man kann somit (ausser man baut eine Rakete) das Ganze betrachten als wäre die Sonne statisch und nur die Erde in Bewegung.

Ein weiteres spannendes Erscheinen der Ellipse im wirklichen Leben tritt in der Form von Flüstergallerien und Flüstergewölben auf. Wenn zwei Menschen in einem elliptischen Raum je in einem Brennpunkt stehen, hören sie sich besonders gut. Der Grund liegt darin, dass die Schallwellen, die aus einem Brennpunkt stammen, an den Wänden abprallen und den anderen Brennpunkt gleichzeitig erreichen. Das wird noch verstärkt unter einem elliptischen Gewölbe.

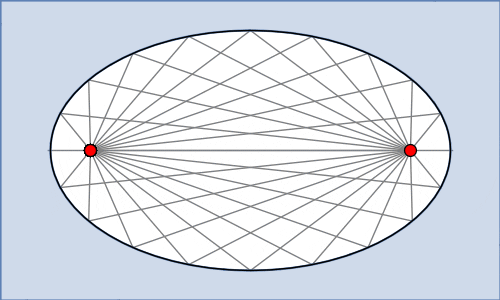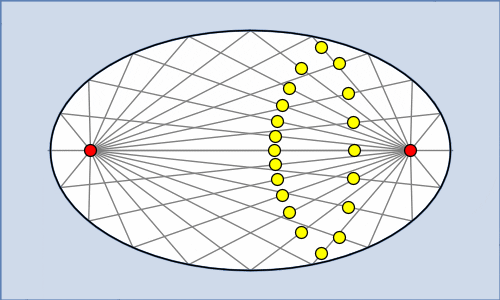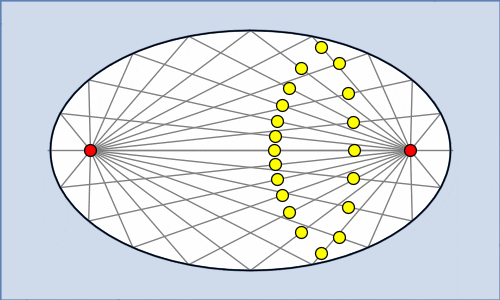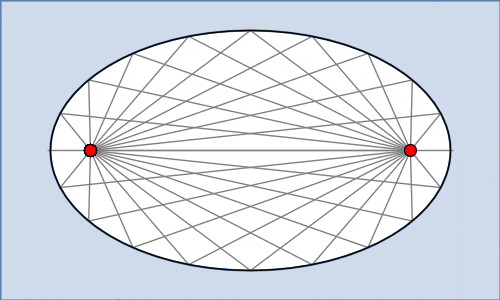
Das Gleiche passiert mit Wasserwellen in einem elliptischen Wassertank oder Lichtstrahlen in einem elliptischen Spiegelraum. Wichtig zu bemerken ist, dass dieses Phänomen nur bei Ellipsen stimmt, und nicht bei jedem Oval; das könnte deswegen auch als definierende Eigenschaft der Ellipse betrachtet werden.

Ellipsen sind auch als abgebildete Kreise aus einer anderen Perspektive zu sehen. Wenn man einen Kreis perspektivisch verzerrt, sieht man eine Ellipse.

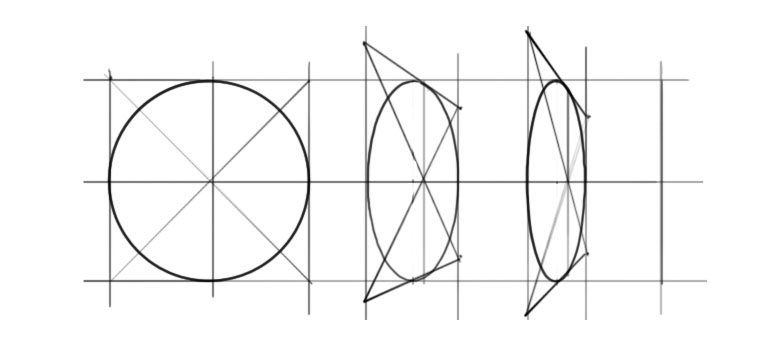Die trockene Mathematik ist nun vorbei und eine willkürliche Auswahl spannender Verwendungen wurde vorgestellt. Übrig bleibt, wie man solche Kurven zeichnen kann, um sie tatsächlich im Instrumentenbau benutzen zu können.

Die einfachste Art, um eine Ellipse zu zeichnen, ist mit einer Schlaufe. Man wickelt sie um zwei Nägel herum und zeichnet mit konstanter Spannung eine Ellipse darum. Falls man die Masse der Halbachsen kennt, und somit eine bestimmte Ellipse zeichnen will, muss man wie folgt vorgehen: Zuerst berechnet man die Distanz zwischen den Brennpunkten. Das ist dank einer einfachen Betrachtung der Symmetrien und dem Satz des Pythagoras einfach zu berechnen:

Jetzt kann man wie vorher vorgehen, mit einer Distanz von zwischen den Nägeln und einer Schlaufe mit der Länge (überlege mal 🙂 ).

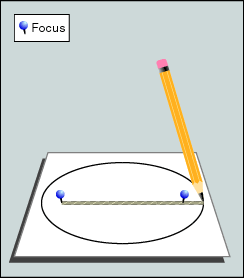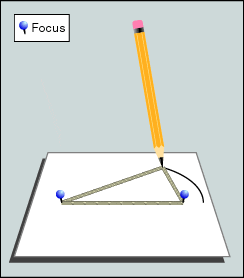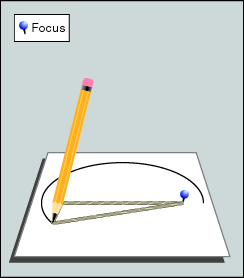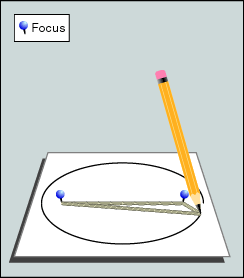
Die Methode ist zwar OK, aber bei kleineren Ellipsen ist die Ungenauigkeit, die aus der Elastizität der Schnur und dem Winkel des Bleistifts stammt, für einen oberpingeligen und mathematisch orientierten Geigenbauer nicht befriedigend.

Eine genialere, historische Methode eine Ellipse zu zeichnen ist mithilfe eines archimedischen Ellipsographs.

Die Konstruktion ist sehr einfach: Sie besteht aus einer Grundplatte mit zwei rechtwinklig zueinander liegenden Führungsnuten und einem Zeichenarm, der zu zwei freibeweglichen Kulissensteinen mit Lagerbolzen verbunden ist. Jeder Kulissenstein bewegt sich in einer unterschiedlichen Nute. Der Zeichenarm schwingt in der Form einer Ellipse. Die Animation hilft wirklich.

Wenn man den Arm parallel zu den Nuten positioniert, sieht man ganz klar, dass die Distanz zwischen dem inneren Stein und dem Bleistift der kleinen Halbachse und der äussere Stein und dem Bleistift der grossen Halbachse entspricht. Schematisch sieht man es in der folgenden Animation, wenn den Arm horizontal und vertikal liegt:

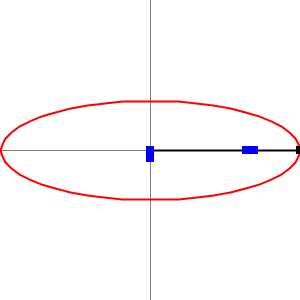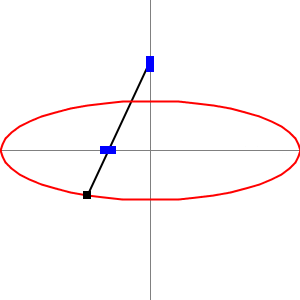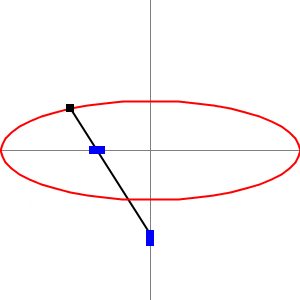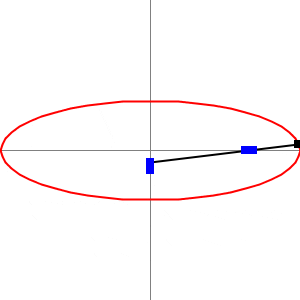
Es bleibt nur noch zu zeigen, dass die abgebildete Kurve tatsächlich eine Ellipse ist. Ein letzter Hauch frische mathematische Luft.

Auch mit wenig trigonometrischer Kenntnis wird es sehr simpel.

Wir drücken die Koordinaten eines allgemeinen in der unterstehenden Abbildung in Bezug auf den Winkel aus, den die bewegliche Stange mit der Hauptachse bildet.

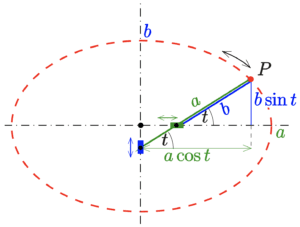
Somit hat jeder die Koordinaten und . Falls diese Koordinaten die Gleichung der Ellipse erfüllen, dann zeichnet eine Ellipse, während es sich um die Grundplatte herum bewegt.

Die Einsetzung der Koordinaten in die Gleichung der Ellipse

ergibt:

Und das stimmt für jeden (und ist auch eigentlich die bekannte trigonometrische Gleichung des Einheitskreises). q.e.d